A REOLOGIA DOS MATERIAIS NO ESTADO SÓLIDO

Marco Antônio de Morais Alcantara 

Duas palavras chave da reologia são: tensão e deformação. Da relação entre estas se pode trazer outras, como energia, coesão interna, e sobretudo, arranjo interno de partículas. Uma deformação pode ser compreendida como resposta a uma tensão aplicada. Diante disso, podemos ter diferentes tipos de respostas, as quais podem definir o carácter destes, e a melhor utilização destes materiais. Serão discutidos alguns comportamentos típicos dos materiais frente ao comportamento dentro das contingências de trabalho. Seguem então os tipos de comportamento, conforme as contribuições mais relevantes. 

 Comportamento linear

Uma dessas respostas é o comportamento linear. No caso do regime linear, existe um comportamento proporcional e linear entre os valores da tensão aplicada, e da deformação. Existe também o retorno das condições originais, uma vez que seja retirado o carregamento.

Uma das características do comportamento linear é o de que a deformação recuperável ocorre com a aplicação da carga, sendo também a relação entre a tensão e a deformação são as mesmas tanto nas fases de carregamento e de descarregamento.

A Figura 1 ilustra as relações entre a tensão e a deformação para o regime elástico.

Figura 1: Relação entre a variação de tensão e de deformação para o sólido que tem o regime linear

Como características do regime linear, a energia absorvida que é absorvida para a sua deformação é capaz de apenas de deslocar átomos, ou de fazer variar a distância entre eles.

Existe energia é armazenada na deformação, pois a distância interatômica nos sólidos é normalmente definida de modo a manter o menor estado de energia; ao aumentar a distância entre os átomos, haverá uma força no sentido de se restabelecer a aproximação, ou, em caso contrário, o sistema promoverá a repulsão entre os átomos. O comportamento linear tem analogia com o de uma “mola”, quando comprimida ou quando tracionada.

Então, existe uma constante de proporcionalidade entre a variação da força e da deformação.

As deformações provocadas durante o regime elástico são consideradas como “deformações instantâneas”.

Os materiais que apresentam o regime elástico são de modo geral materiais que apresentam ligações fortes.

 

Comportamento plástico e elastoplástico

O comportamento elastoplástico e o plástico se caracterizam pelo fato de que o material não apresenta mais o retorno às suas condições originais, quando é retirado o carregamento. Permanecem deformações residuais quando efetuado o descarregamento, as quais se constituirão em “deformações permanentes”. Aliás, o conceito de “plástico” advém da conformação e da conservação da forma após um esforço aplicado.

No regime plástico ocorre com a ruptura de ligações, ou com concomitante rearranjo em sua microestrutura interna, no sentido de buscar se reservas.

Dois aspectos importantes para os materiais no regime plástico são o escoamento e o limite de resistência, sendo exemplificado, por exemplo, com o caso dos aços, o qual explora um rearranjo interno, permitido mediante um deslocamento de planos atômicos, que conduz a um revigoramento, até a ruptura.

Inicialmente o tipo de comportamento induzido ao material é o regime elástico, sendo, então, são alcançados os estados elastoplásticos e plásticos, a partir de um determinado nível de tensão aplicada. O nível de tensão aplicado para se alcançar o estado plástico é a “tensão de escoamento”.

As deformações decorrentes do estado plástico ou elastoplásticas não são recuperáveis.

As Figuras 2 e 3 ilustram o comportamento do estado plástico. 

Figura 2: Relação entre a variação de tensão e de deformação para o sólido que tem o regime elastoplástico

 

Figura 3: Relação entre a variação de tensão e de deformação para o sólido que tem o regime plástico

Fluência e relaxação

Diferentemente do aspecto da variação da deformação somente com o valor da tensão, pode-se incluir também o tempo. Um tipo de deformações pode ser caracterizado como o resultado da ação de um carregamento imposto durante um determinado intervalo de tempo, onde, o aumento desta deformação pode ocorrer sem que o valor da carga varie. Estas deformações são conhecidas como “fluência”. Podem ocorrer em materiais diversos, variando-se as condições que as favoreçam. A Figura 4 apresenta um exemplo de material solicitado à esforço de tração, onde, após determinado nível de carga, este apresenta variações dimensionais sem que ocorram níveis de tensão compatíveis com estas deformações. Diz-se que o material "flui". 

Figura 4: Fenômeno da fluência

Outro conceito é o de "relaxação", caracterizado pelo alívio e tensões, gradativamente com o tempo, mesmo sem variar a carga. Este fenômeno é ilustrado através da Figura 5. 

Figura 5: Fenômeno da relaxação

Materiais viscoelásticos

De modo geral os materiais têm sido compreendidos pela característica de comportamento de dar uma resposta imediata à solicitação mecânica, implicando em deformações instantâneas. Os materiais viscoelásticos já apresentam como comportamento o de necessitar de uma variação no tempo para o ajuste a uma solicitação por tensão, e a este tipo de comportamento se dá o nome de “deformação viscosa”. A deformação viscoelástica ocorre com variação do valor da carga, e enquanto durar a aplicação da carga, esta permanecerá, mesmo que esta carga não sofra variação, assim como, necessitam de um tempo para a relaxação de tensões.

O comportamento viscoelástico pode ser definido como a conjunção do comportamento elástico com o comportamento viscoso, permitindo uma deformação viscoelástica recuperável, ou ainda esta pode ser também a conjunção de um comportamento plástico e viscoso, não recuperável, ou ainda, elastoviscoplástico.

Os materiais viscoelásticos apresentam o fenômeno de relaxação, onde as tensões internas são diminuídas, mesmo sem a variação da deformação.

 

Materiais frágeis e materiais dúcteis

Os materiais podem apresentar comportamentos que podem ser enquadrados como “frágeis” ou como “dúcteis”, além do viscoelástico, como citado por último. Isto, visto conforme eles possam apresentar deformações além do limite elástico, assim como possam apresentar um aviso prévio dizendo que a ruptura está por vir, ou ainda, pode ser distinguida a fluência.

Os materiais frágeis tendem a apresentar a ruptura de modo brusco, e instantâneo, enquanto que a ruptura dúctil normalmente é precedida de deformações.

Como exemplos de materiais frágeis têm-se os materiais cerâmicos e os concretos, os vidros, alguns polímeros rígidos, enquanto que, como material dúctil tem-se os aços, e os polímeros.

Como fatores contribuintes para a fragilidade dos materiais podem ser citados: heterogeneidade, falta de isotropia, descontinuidades causadas pelos poros e pelas fissuras, concentração de tensões, e, para os casos dos materiais dúcteis podem ser destacadas a homogeneidade e o reflexo mediante o comportamento homogêneo de tensões e de deformações, sejam de origens mecânicas ou térmicas, e ainda, o tipo de microestrutura interna.

Podemos ilustrar os exemplos dos materiais cerâmicos e dos materiais metálicos. Ambos são constituídos por ligações fortes. No caso dos materiais cerâmicos, a pluralidade mineralógica, a possível presença de grãos de areia, de materiais diferenciados como cristalinos e amorfos, conduz a um contexto favorável para a ocorrência de concentrações de tensão, e da consequente ruptura por ação de forças internas de tração. No caso dos materiais metálicos, cabem ser considerados os casos dos aços e dos ferros fundidos. O aço apresenta melhor distribuição de carbono nas estruturas do ferro, permitindo maior maleabilidade, enquanto que no caso do ferro fundido, tanto a concentração de carbono é maior, assim como é menor a sua dissolução na estrutura do ferro, permitindo a sua concentração, acúmulo, e a formação de uma estrutura heterogênea.

De modo geral, os mecanismos finais de ruptura em materiais frágeis são comandados por esforços internos de tração, enquanto que, para os materiais dúcteis, de cisalhamento interno.

A Figura 6 ilustra o comportamento dos materiais quanto ao carácter de ductilidade, de fragilidade ou de fluência.

 

 Figura 6:Comportamento dos materiais quanto ao carácter de ductilidade ou de fragilidade ou de fluência

 A energia requerida pelos materiais durante a ruptura

Os materiais não são levados à ruptura por solicitações externas ou internas, ocorre uma intervenção que possibilita realizar o distanciamento e a quebra de ligações, e de partes da microestrutura.

A isto se pode associar a energia que é dispensada durante estas intervenções, de modo que possam conduzir à ruptura deste.

Do trabalho (avaliado em termos e energia) representado pela atuação da tensão, com a respectiva deformação, têm-se a energia envolvida no processo. Este valor de energia corresponde ao que é a “tenacidade” do material, sendo expressa pela área sob a curva que representa a tensão contra a deformação. A Figura 7 ilustra a tenacidade.

Figura 7: Quantificação da energia absorvida na ruptura

É importante ressaltar que a tenacidade não é a mesma coisa que o “limite de resistência” de um material, mas sim, a forma que os mecanismos de resistência imporão na ruptura, absorvendo energia. Neste sentido, pode até existir o caso de que um material que apresente um limite de ruptura mais baixo requeira maior quantidade de energia, do que outro que apesente um limite maior de ruptura. Isto pode ser ilustrado pela Figura 8.

Figura 8: Comparação entre casos de energia absorvida na ruptura

A tenacidade dependerá da estrutura da estrutura interna do material. No caso do concreto, a presença de fibras em sua composição poderá colaborar para o aumento da tenacidade.

 

Modelos físicos para as relações entre tensões e deformações tanto instantâneas instantâneas como à longo prazo

Algumas analogias com modelos físicos têm sido utilizadas para poder explicar o comportamento reológico dos materiais.

O comportamento elástico pode ser comparado ao caso de atuação de uma “mola”. Conhecido é das leis da física de que uma mola, ao ser tracionada, tende a oferecer uma força restauradora, de modo a que esta possa retornar às condições originais. Também é conhecido que existe uma constante elástica, que associa a deformação da mola com a força restauradora.

Para o caso dos materiais, à constante da mola existe uma correspondente, o módulo de elasticidade, dado por "E". Desta forma tem-se que:

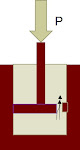
Para o caso do regime plástico, por sua vez, se pode adotar a ideia do arraste de um bloco sobre uma superfície dotada de atrito. A força necessária para iniciar o deslocamento do bloco deverá vencer o atrito interno e as forças de inércia, quando, então, o deslocamento se iniciará, sendo a deformação permanente mesmo após o término da aplicação da força. Na Figura 9 é ilustrada a ideia de que existe inicialmente um deslocamento dentro do regime elástico, passado, então, a se romper com o regime elástico, quando vencidas as forças de inércia.

Figura 9: Modelo de comportamento para o regime plástico

O comportamento viscoso é representado por meio da analogia do modo de atuação de um pistão. Um “embolo” atua em um meio onde se dispõe de um fluido confinado, o qual pode atravessar esse êmbolo mediante uma abertura; da aplicação do esforço sobre o êmbolo, e da facilidade de passagem do líquido pela abertura, se dará o deslocamento do êmbolo. Este deslocamento se dará em maior magnitude mediante o aumento da força aplicada, e da viscosidade embutida no sistema. A Figura 10 ilustra o pistão, concebido de modo a poder atuar como um amortecedor, quando aplicada uma carga.

Figura 10: Pistão idealizado para representar o comportamento viscoso

Uma analogia para explicar o comportamento dos materiais viscoelásticos é dada admitindo-se que eles reúnem o comportamento de uma “mola” e de um “pistão”, sendo a mola utilizada para induzir o comportamento elástico, e o pistão para o comportamento viscoso.

A Figura 11, ilustra os ícones utilizados na literatura para representar os casos da mola (elástica) e do pistão (amortecedor).

Figura 11: Ícones utilizados para representar os modelos elásticos e viscosos

Os modelos apresentados pela literatura têm sido aqueles em que os elementos mola e pistão possam estar associados em série, ou em paralelo, Figura 12 e Figura 13, com as contingências de se ter, para os casos de associação em série a mesma tensão, e para os casos de associação em paralelo, se tem a mesma deformação, com diferentes tensões nos elementos.

Figura 12: Modelo de atuação em paralelo para representar os fenômenos elásticos e viscosos

Figura 13: Modelo em série para representar os fenômenos elásticos e viscosos

A Figura 14 apresenta as equações constitutivas, cinética e cinemática são apresentadas a seguir para os casos de modelos admitindo-se associação em paralelo, conhecidos como modelos de Kelvin.

Figura 14: Equações constitutivas para o modelo em paralelo, de Kelvin

Pode-se observar que a deformação varia em função do tempo e depende de propriedades elásticas do material e das propriedades viscosas. A tensão resultante sobre o material é equivalente à soma das tensões induzidas nos elementos elásticos e viscosos.

A Figura 15 ilustra as variações de tensão, com uma aplicação da carga em t₀, manutenção desta até o tempo dado por t₁, com o seu descarregamento neste instante, e a variação da deformação entre o intervalo de tempo entre t₀ e  t₁, assim como a variação da tensão após o descarregamento.

Figura 15: Comparação entre quadros de tensão, deformação e relaxamento para o modelo de Kelvin 

Observa-se que a deformação varia assintoticamente para o valor de σ₀ /E, a qual representa o valor da deformação elástica. A deformação se processa mediante o regime de fluência, sem a necessidade do aumento do valor da tensão aplicada. O trecho seguinte ao tempo t1 representa o trecho após o descarregamento e a ocorrência da relaxação.

A trajetória de eventos se dá aparentemente da seguinte forma:

No início, no trecho relativo à fluência, toda carga é absorvida pelo amortecedor, o qual se deforma gradativamente, enquanto está aliviada de tensões. A medida que o tempo passa, ocorre a transferência de tensão do amortecedor para a mola, sendo a tensão diminuída neste, como a velocidade de deformação. Ocorre então a tendência de que a deformação será anulada com a tensão total suportada pela mola, dentro do modelo assintótico ilustrado.

Na fase de recuperação, se admite que a deformação resultante induz tensão na mola, a qual é compensada por outra, de sinal contrário, oriunda do amortecedor. Desta forma ocorre a recuperação da deformação, a qual diminui concomitantemente com a deformação ocorrida.

A velocidade da deformação é assintótica tendendo para o eixo das abscissas, de modo a se ter o valor nulo.

Quanto ao modelo de associação em série, concebido por Maxwell, as equações constitutivas estão apresentadas na Figura 16, e a comparação entre a trajetória de carregamento e de deformação é apresentada nas Figura 17 e 18.

Figura 16: Equações constitutivas para o modelo em paralelo, de Maxwell

Figura 17: Modelo de Maxwell, fase de carregamento e fluência

Figura 18: Modelo de Maxwell, fase de relaxação

Observa-se que a deformação resultante é igual à soma das componentes elásticas e viscosas, e que a tensão atuante á igual.

Das figuras apresentadas, a Figura 17 destaca a fase da fluência, enquanto que a Figura 18 cuida da fase da relaxação.

Pode-se observar que existem componentes relativas às propriedades elásticas e viscosas, assim como, a parcela referente aos componentes elásticos é recuperável, e que, a parcela referente à viscosidade sobre variação com a diminuição gradual da tensão ao longo do relaxamento.

No modelo físico, no momento da aplicação da carga a tensão é suportada totalmente pela mola, resultando no valor de Eε₀. Com a transferência, ocorre a dissipação da tensão e anulação.

Bibliografia:

ANDRADE, J.J.O; PASSAN.E Propriedades físicas e mecânicas dos materiais In: MATERIAIS DE CONSTRUÇÃO CIVIL E PRINCÍPIOS DE CIÊNCIAS DOS MATERIAIS. Geraldo Isaia/IBRACON, São Paulo, 2017, pp.226-259

GERE, J.M; GOODNO, B.J Mecânica dos materiais. São Paulo, 2017, 497p.

SILVA, D.V Mecânica e resistência dos materiais Coimbra, 2004, Zuari-Edição de Livros Técnicos, pp. 63-70